This project was a continuation of my previous wave and burgers equations solver. Here, the Euler equations are the ones being numerically solved. Some basic ideas still apply: discontinuities generate numerical instabilities that can contaminate the overall solution so there must be some kind of dissipation, at least at the discontinuities regions, that should stop instabilities from growing. On the other hand, if too much dissipation is present, high frequency waves will be damped. It is a balance between dissipation, resolution and computational cost. Although the problems studied here are simple 1D cases, interesting insights can be gathered for more complex problems, such as turbulent flows.
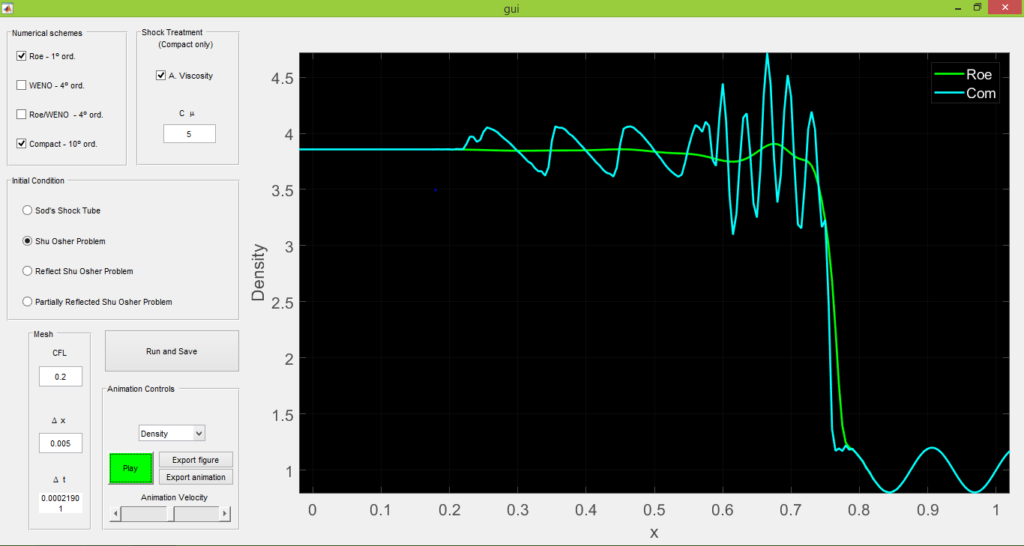
This GUI has the objective of showing how different numerical schemes may be (or not) suited for different situations where shocks and high frequency oscillations are present. Just run the gui.m file and you are good to go. After choosing a set of parameters, the simulations are performed and the output data is saved in your working directory. You can play an animation for those parameters after the simulations are done by pressing the button “Play”. The following numerical methods can be chosen:
• Roe Flux Differencing Scheme (1st order)
• WENO (4th order)
• Hybrid Roe/WENO scheme (4th order)
• Compact (10th order)
The Compact scheme has an additional setting for artifical viscosity, which is added on regions with large gradients (discontinuities). This allows this scheme to be used in situations with shocks while retaining its original accuracy for most regions.
It is clear that there is no “better” numerical scheme. For example, the Roe scheme (1st order) has a lot dissipation but if dealing mainly with shocks it might be good enough or serve as a first “draft” of how the solution looks like (it is computationally the cheapest scheme to use). If properly solving the high frequency components is the main interest, the compact scheme is more appropriate for that. However if the region near the shock is also important, the WENO scheme exhibits a good balance and requires less parameter tuning.