Static Stall
When there is a flow going through an airfoil with a certain angle of attack α, a low pressure region is created at the top side (suction side) and a high pressure one at the bottom (pressure side). Since this difference in pressure exists, a resultant force is created. This force has vertical (lift) and horizontal (drag) components.
As you increase the angle of attack, this pressure difference gets higher and higher, which will create a stronger resultant force, increasing mostly lift but also drag. However, after a certain angle, lift will suddenly begin to drop. At this moment it is said that the airfoil is stalled.
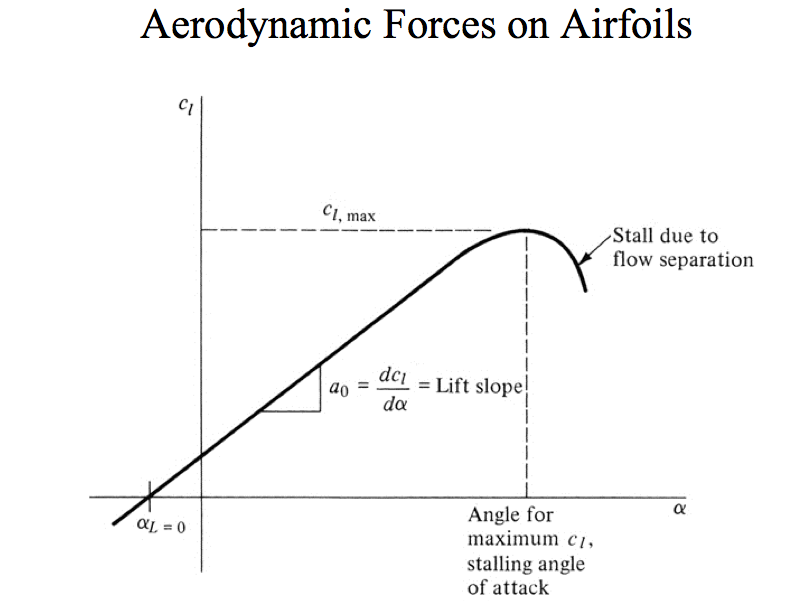
This drop happens because the flow becomes separated and stops “touching” the whole airfoil. The steeper the angle of attack, the more pronounced this effect is. Below there are some high fidelity simulation results for a SD7003 airfoil with different angles of attack. The yellow moving spheres can be interpreted as a fluid particle at that location. Blue colored regions represent a low pressure zone while red colored ones represent a high pressure one.
The flow is simulated through a lot of time steps and then averaged to get rid of fluctuations caused by turbulence. As it can be seen, at 8° there is a recirculation bubble near the leading edge but most of the flow is attached to the airfoil. At 15°, there is a huge separation region and the airfoil is without a doubt stalled. If the angle of attack is increased even more, the separation region grows even bigger and another recirculation zone also appears at the airfoil wake.
When you zoom at the leading edge, it is possible to see small recirculation zones for all cases. Many parameters influence those bubbles’ characteristics, like Reynolds number, Mach number, angle of attack, airfoil geometry, etc. The physics behind those bubbles are studied until this day because of its important role in many fluid phenomena, e.g. dynamic stall. Keep in mind that these results are time averages of the LES simulations, which explains why the solutions are so smooth.