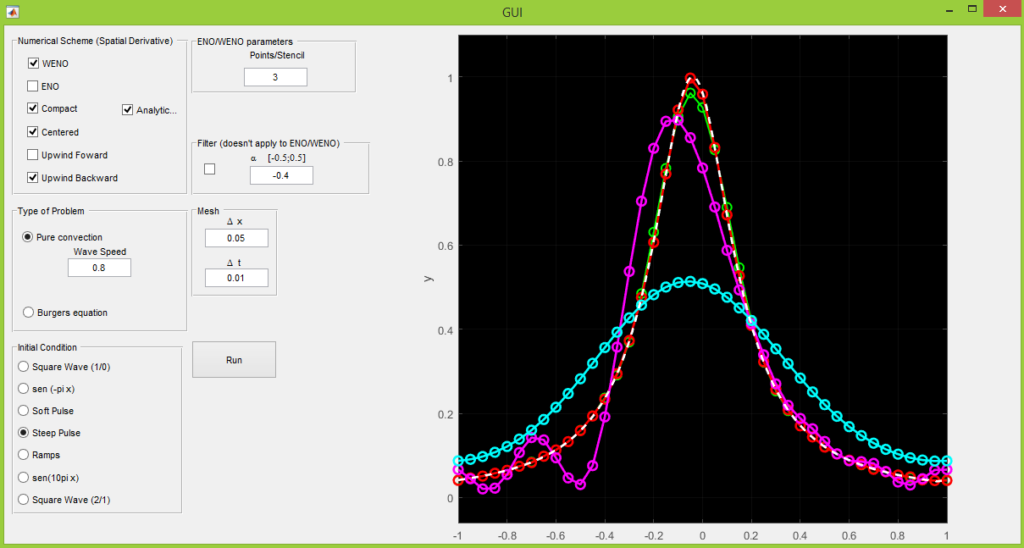
This project had the aim to study the behavior of different numerical schemes for spatial derivatives, being more of a educational tool. It was awarded as one of the best undergraduate research projects amongst all developed in 2015 at the University of Campinas. The main goal was to understand the trade off between high order accuracy and the need of dissipation when considering solutions with high frequency components as well as discontinuities. You just need to run the GUI.m file and that’s it. The order of accuracy of the methods are

• WENO (4th or 2nd order)
• ENO (2nd or 1st order)
• Compact (6th order)
• Centered (2nd order)
• Upwind (1st order)

After running different initial conditions it should be clear that higher order methods are well suited to capture high frequencies components but accomplish that by having little dissipation. This can be a problem when discontinuities are part of the solution. In this scenario, numerical oscillations will will appear (Gibbs phenomenon) and more dissipative methods would be more appropriate. WENO schemes aim to address this problem by computing derivatives with higher order in smooth regions and with low order (adding dissipation) in regions with discontinuities. However, this comes at a cost of being more computationally expensive.

The code organization is very rudimentary (it was my first code) and I would need a considerable amount of time to polish it nowadays. In this way, I recommend anyone to check it out only if there is no intentions of actually adding new features but just using it for educational purposes.